- -The beam is originally straight, and any taper is slight
- -The beam experiences only linear elastic deformation
- -The beam is slender (its length to height ratio is greater than 10)
- -Only small deflections are considered (max deflection less than 1/10 the span.
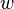 ) can be approximated as:
) can be approximated as: is interpreted as its curvature,
is interpreted as its curvature,  is the Young's modulus,
is the Young's modulus,  is the area moment of inertia of the cross-section, and
is the area moment of inertia of the cross-section, and  is the internal bending moment in the beam.
is the internal bending moment in the beam.If, in addition, the beam is not tapered and is homogeneous, and is acted upon by a distributed load
 , the above expression can be written as:
, the above expression can be written as:Cantilever beams
Cantilever beams have one end fixed, so that the slope and deflection at that end must be zero.
Schematic of the deflection of a cantilever beam.
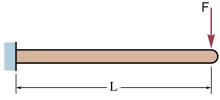
End-loaded cantilever beams
Cantilever beam with a force on the free end
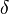 and angle of deflection
and angle of deflection  (in radians) at the free end in the example image: A (weightless) cantilever beam, with an end load, can be calculated (at the free end B) using:[1]
(in radians) at the free end in the example image: A (weightless) cantilever beam, with an end load, can be calculated (at the free end B) using:[1] = Force acting on the tip of the beam
= Force acting on the tip of the beam = Length of the beam (span)
= Length of the beam (span) = Modulus of elasticity
= Modulus of elasticity = Area moment of inertia of the beam's cross section
= Area moment of inertia of the beam's cross section
 , along the span of an end loaded cantilevered beam can be calculated using:[1]
, along the span of an end loaded cantilevered beam can be calculated using:[1] (the end of the beam), the
(the end of the beam), the  and
and 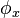 equations are identical to the
equations are identical to the  and
and 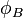 equations above.
equations above.Uniformly-loaded cantilever beams
Cantilever beam with a uniform distributed load
 = Uniform load on the beam (force per unit length)
= Uniform load on the beam (force per unit length) = Length of the beam
= Length of the beam = Modulus of elasticity
= Modulus of elasticity = Area moment of inertia of cross section
= Area moment of inertia of cross section
 , along the span of a uniformly loaded cantilevered beam can be calculated using:[1]
, along the span of a uniformly loaded cantilevered beam can be calculated using:[1]Simply-supported beams
Simply-supported beams have supports under their ends which allow rotation, but not deflection.
Schematic of the deflection of a simply-supported beam.
Center-loaded simple beams
Simply-supported beam with a force in the center
 = Force acting on the center of the beam
= Force acting on the center of the beam = Length of the beam between the supports
= Length of the beam between the supports = Modulus of elasticity
= Modulus of elasticity = Area moment of inertia of cross section
= Area moment of inertia of cross section
 , along the span of a center loaded simply supported beam can be calculated using:[1]
, along the span of a center loaded simply supported beam can be calculated using:[1]Off-center-loaded simple beams
Simply-supported beam with a force off center
 from the closest support, is given by:[1]
from the closest support, is given by:[1] = Force acting on the beam
= Force acting on the beam = Length of the beam between the supports
= Length of the beam between the supports = Modulus of elasticity
= Modulus of elasticity = Area moment of inertia of cross section
= Area moment of inertia of cross section = Distance from the load to the closest support (i.e.
= Distance from the load to the closest support (i.e. 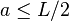 )
)
 from the closest support and is given by:[1]
from the closest support and is given by:[1]Uniformly-loaded simple beams
Simply-supported beam with a uniform distributed load
 = Uniform load on the beam (force per unit length)
= Uniform load on the beam (force per unit length) = Length of the beam
= Length of the beam = Modulus of elasticity
= Modulus of elasticity = Area moment of inertia of cross section
= Area moment of inertia of cross section
 , along the span of a uniformly loaded simply supported beam can be calculated using:[1]
, along the span of a uniformly loaded simply supported beam can be calculated using:[1]Units
The formulas supplied above require the use of a consistent set of units. Most calculations will be made in SI or US customary units, although there are many other systems of units.International system (SI)
- Force: newtons (
 )
)
 )
)- Modulus of elasticity:
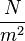
- Moment of inertia:

US customary units (US)
- Force: pounds force (
 )
) - Length: inches (
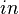 )
) - Modulus of elasticity:
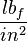
- Moment of inertia:
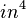
Others
Other units may be used as well, as long as they are self-consistent. For example, sometimes the kilogram force ( ) unit is used to measure loads. In such a case, the modulus of elasticity must be converted to
) unit is used to measure loads. In such a case, the modulus of elasticity must be converted to 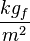 .
.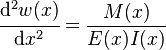
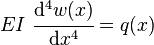



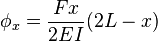


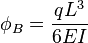
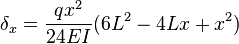
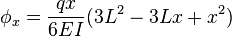


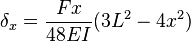
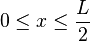

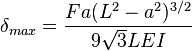
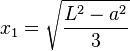



No comments:
Post a Comment