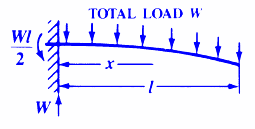
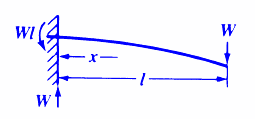
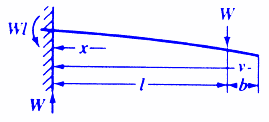
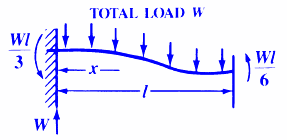
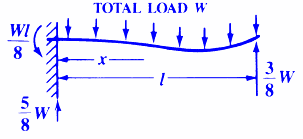
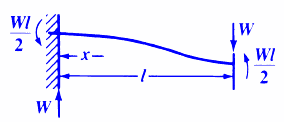
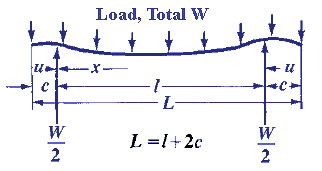
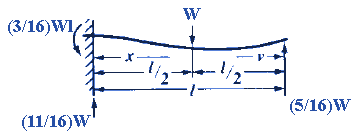
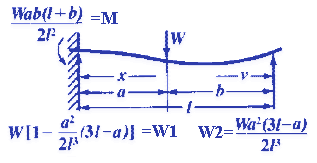
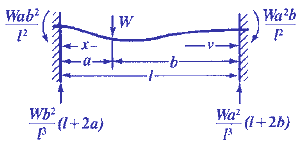
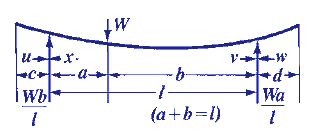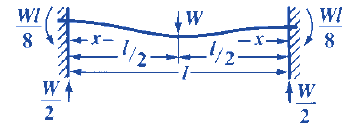INITIAL & FINAL SETTING TIME
We need to calculate the initial and final setting time as per IS: 4031 (Part 5) – 1988. To do so we need Vicat apparatus conforming to IS: 5513 – 1976, Balance, whose permissible variation at a load of 1000g should be +1.0g, Gauging trowel conforming to IS: 10086 – 1982.
Procedure to determine initial and final setting time of cement
i) Prepare a cement paste by gauging the cement with 0.85 times the water required to give a paste of standard consistency.
ii) Start a stop-watch, the moment water is added to the cement.
iii) Fill the Vicat mould completely with the cement paste gauged as above, the mould resting on a non-porous plate and smooth off the surface of the paste making it level with the top of the mould. The cement block thus prepared in the mould is the test block.
A) INITIAL SETTING TIME
Place the test block under the rod bearing the needle. Lower the needle gently in order to make contact with the surface of the cement paste and release quickly, allowing it to penetrate the test block. Repeat the procedure till the needle fails to pierce the test block to a point 5.0 ± 0.5mm measured from the bottom of the mould.The time period elapsing between the time, water is added to the cement and the time, the needle fails to pierce the test block by 5.0 ± 0.5mm measured from the bottom of the mould, is the initial setting time.
B) FINAL SETTING TIME
Replace the above needle by the one with an annular attachment. The cement should be considered as finally set when, upon applying the needle gently to the surface of the test block, the needle makes an impression therein, while the attachment fails to do so. The period elapsing between the time, water is added to the cement and the time, the needle makes an impression on the surface of the test block, while the attachment fails to do so, is the final setting time.
We need to calculate the initial and final setting time as per IS: 4031 (Part 5) – 1988. To do so we need Vicat apparatus conforming to IS: 5513 – 1976, Balance, whose permissible variation at a load of 1000g should be +1.0g, Gauging trowel conforming to IS: 10086 – 1982.
Procedure to determine initial and final setting time of cement
i) Prepare a cement paste by gauging the cement with 0.85 times the water required to give a paste of standard consistency.
ii) Start a stop-watch, the moment water is added to the cement.
iii) Fill the Vicat mould completely with the cement paste gauged as above, the mould resting on a non-porous plate and smooth off the surface of the paste making it level with the top of the mould. The cement block thus prepared in the mould is the test block.
A) INITIAL SETTING TIME
Place the test block under the rod bearing the needle. Lower the needle gently in order to make contact with the surface of the cement paste and release quickly, allowing it to penetrate the test block. Repeat the procedure till the needle fails to pierce the test block to a point 5.0 ± 0.5mm measured from the bottom of the mould.The time period elapsing between the time, water is added to the cement and the time, the needle fails to pierce the test block by 5.0 ± 0.5mm measured from the bottom of the mould, is the initial setting time.
B) FINAL SETTING TIME
Replace the above needle by the one with an annular attachment. The cement should be considered as finally set when, upon applying the needle gently to the surface of the test block, the needle makes an impression therein, while the attachment fails to do so. The period elapsing between the time, water is added to the cement and the time, the needle makes an impression on the surface of the test block, while the attachment fails to do so, is the final setting time.