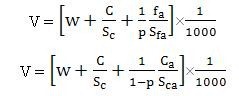rtcomings of the Davisson Offset Limit Applied to Axial Compressive Load
Tests on Cast-In-Place Piles
W. Morgan NeSmith, Member, Geo-Institute1
Timothy C. Siegel, P.E., Member, Geo-Institute2
1 Berkel & Company Contractors, Inc., 834 Dekalb Avenue, Unit B, Atlanta, GA 30307, PH (865) 528-
1653, email: morgan_nesmith@comcast.net
2 Berkel & Company Contractors, Inc., 1808 Northshore Hills Boulevard, Knoxville, TN, 37922, PH
(865) 357-1715, FAX (865) 357-1570, email: tcsiegel@knology.net
ABSTRACT
Since its introduction in 1973, the Davisson Offset Limit has been widely used in the
United States for interpretation of axial compressive load tests on pile foundations and is
one of three methods explicitly accepted by the 2006 International Building Code. An
examination of the fundamental assumptions of the DOL shows that its application to
cast-in-place piles lacks scientific basis and leads to over conservatism. Interestingly,
these are the same reasons given by Davisson for its development. The results of the
examination indicate that there are notable fallacies in the Davisson Offset Limit,
including the assumptions that: (1) the cast-in-place pile behaves as a “fixed-base,
free-standing column.”, (2) an elastic line is a dependable reference line for
interpretation of load tests on cast-in-place piles, and; (3) an offset of 3.8 mm + D
(inches)/120 from the elastic line represents the movement necessary to mobilize toe
resistance of cast-in-place piles. Considering these results, the authors present
suggestions ranging from modifications to the Davison Offset Limit that recognizes
the greater movement required to mobilize the toe resistance to codification of a more
rational criterion better suited to interpret the axial compressive capacity of cast-inplace
piles.
INTRODUCTION
The 2006 International Building Code explicitly accepts three interpretive methods for
axial compressive load tests on piles. These three interpretative methods (by the names
they are used in common vernacular): (1) Davisson Offset Limit (Davisson, 1972); (2)
Brinch Hansen 90% Criterion (Brinch Hansen, 1963), and; (3) Butler-Hoy Criterion
(Butler and Hoy, 1977). Generally speaking, the Davisson Offset Limit (DOL) is
frequently used in the United States because it provides the lowest estimation of axial
compressive capacity of the aforementioned methods. Also, it is most likely to provide
an ultimate axial compressive pile capacity from the actual load-deflection curve. That
is, the Brinch Hanson 90% Criterion and the Butler-Hoy Criterion often require
extrapolation to extend the load-deflection curve in order to establish an ultimate axial
compressive capacity. In the absence of established guidelines for extrapolation, there
is a reluctance, and even opposition, to the extrapolation of load test results.
568 DEEP FOUNDATIONS
568
2
Its widespread application to all pile types in the US is sufficient justification for a
critical examination of the appropriateness of the DOL, especially for the evaluation of
load tests results for cast-in-place piles. The first part of this paper discusses the
fundamentals that were involved in the formulation of the DOL and the fallacies
associated with its application to load testing of cast-in-place piles. The second part of
this paper presents examples of results from actual load tests that serve to illustrate the
shortcomings of the DOL with respect to actual pile behavior and application to
design. The third and final part of this paper presents suggestions for load test
procedures and interpretation in light of the current understanding of geotechnical
engineering.
FUNDAMENTALS OF THE DAVISSON OFFSET LIMIT
The Davisson Offset Limit (as it is currently referred to) was proposed by Davisson
(1972) based on comparisons between the results of wave equation analyses of driven
steel piles and static load tests. The DOL defined the ultimate pile load as the
intersection of the pile load-deflection curve with an elastic line for a fixed-base, freestanding
column offset by 3.8 mm (0.15 inches) plus the soil quake. Soil quake is the
deformation (or pile movement) required to mobilize the strength of the soil below the
pile tip. The soil quake is further simplified by the pile diameter (in inches) divided by
120. In his 1972 paper, Davisson is explicit that the criterion was developed for point
bearing driven piles but goes on to state that it can also be applied to friction piles.
Davisson explains his motivation in the paper’s introduction:
“There are many ways of interpreting a load test; almost all of them are unsatisfactory for high
capacity piles. It appears that engineering practice is based primarily on experience, precedent,
and perhaps prayer, even for low capacity piles. Because of the inadequate basis for practice,
engineers tend toward over-conservatism in design; often this causes unnecessary problems.
When the present day need for high capacity piles is considered in light of the state of practice
with low capacity piles, it is obvious that engineers more than ever need a scientific basis for
their engineering decisions.”
FALLACIES OF THE DAVISSONS OFFSET LIMIT
Davisson was clearly aware of the challenges with load test interpretation and
particularly, the tendency of the engineering community to accept over-conservatism in
establishing the ultimate pile capacity. Ironically, the application (or misapplication) of
the DOL to cast-in-place piles has not only led to greater conservatism but it fails as a
rational, scientific criterion. The primary fallacies of the application of the DOL to
cast-in-place piles are discussed in the following:
(1) The assumption that the cast-in-place pile behaves as a “fixed-base, freestanding
column.” Cast-in-place are generally designed using a combination
of shaft and end resistances and the stress distribution in the pile element is
unlike the “fixed-base, free-standing column” assumed by the DOL. This is
especially true at test loads well below the ultimate capacity where the
resistance is primarily developed along the shaft.
DEEP FOUNDATIONS 569
569
3
(2) The assumption that an elastic line is a dependable reference line for
interpretation of load tests on cast-in-place piles. Kulhawy and Chen (2005)
compared the estimated elastic shortening, based on the assumptions of the
DOL, to the initial slope of the straight line portion of the load-deflection
curve. Their study concluded that the DOL assumptions tended to overestimate
the stiffness of short piles and underestimate the stiffness for longer piles.
(3) The assumption that an offset of 3.8 mm + D (inches)/120 from the elastic
line represents the movement necessary to mobilize toe resistance. The soil
quake proposed by Davisson is specifically for driven piles and is not
appropriate where soil resistance beneath the pile toe has not been fully
mobilized at the beginning of load testing. That is, Davisson study evaluated
piles installed by driving where a compressed soil plug forms during
placement. In contrast, cast-in-place piles and other types of drilled piles do
not compress the soil beneath the pile toe during installation. Thus, a greater
downward movement of the pile toe would be required to mobilize the end
resistance for cast-in-place piles if all other conditions were equal. Analysis
by Zheng et al. (2007) confirmed this based on results of load tests performed
on displacement cast-in-place piles.
EXAMPLE LOAD TEST ANALYSES
Osceola, Arkansas Site
It is helpful to illustrate the shortcomings of the DOL using examples of actual load
test results. For this purpose, we have selected test data from a load test performed by
Berkel & Company Contractors, Inc. (Berkel) and published by Zheng et al. (2007).
The data were collected during a quick load test (ASTM D1143) performed on a 457
mm (18 in) diameter displacement cast-in-place pile with a length of 12.8 m (42 ft).
The load-deflection data are shown in Figure 1. Refer to the paper by Zheng et al.
(2007) for details concerning the geotechnical conditions at the test site.
The DOL is illustrated by two lines in Figure 1. In this case, the elastic line was
intentionally fit to the initial straight line portion of the load-deflection curve and
corresponds to a slope of 37,200 MPa (5.4 x 106 psi). Intuitively, if the fundamental
assumptions of the DOL are valid, then the combined modulus (i.e., both grout and
reinforcing steel) should closely correspond to the slope of the initial straight line
portion of the load-deflection curve. In fact, strain gage measurements obtained in the
upper portion of the cast-in-place pile indicate a combined modulus ranging from
about 27,500 to 34,500 MPa (4 to 5 x 106 psi) which is significantly smaller than the
slope of the straight line portion. This shows that not only does the DOL fail to
appropriately represent a pile with substantial shaft resistance, but also suggests that
selection of the appropriate modulus becomes problematic due to the stress-dependant
non-linearity of the pile materials.
The DOL line was constructed by offsetting the elastic line by a distance of 3.8 mm
(0.15 inches) plus the pile diameter in inches divided by 120. According to the DOL,
the axial compressive capacity of the pile is 2200 kN (450 kips). However, it is clear
570 DEEP FOUNDATIONS
570
4
that the pile is capable of resisting additional compressive load up to 2850 kN (640
kips) at which point the test load was removed. It is recognized that Davisson (1993)
proposed that the pile width (and thus the soil quake term) be multiplied by a factor of
2 to 6 for drilled piles in recognition of the greater pile movement that is required to
mobilize the toe resistance. However, such a modification has yet to be formally
established in those codes that specify the DOL, and as a result, incorporation of such a
modification has not been widespread in engineering practice. Also, the different
modifier values results in a wide range of pile capacity interpretations.
Des Moines, Iowa Site
A second example is from a load test performed by Berkel in Des Moines IA. The data
were collected during a quick load test (ASTM D1143) performed on a 457 mm (18 in)
diameter displacement pile with a length of 12.8 m (34.5 ft). The subsurface conditions
at the pile location are characterized by a stiff fine-grained soil to about 6.1 m (20 ft)
depth underlain by loose to dense clean sands. The load-deflection data are shown in
Figure 2 along with a summary of ultimate load analysis methods. The methods
include the three specifically listed in IBC 2006 as well as a method proposed by
NeSmith (2002). This method was developed from a database of drilled, cast-in-place
piles, and is based on defining ultimate load such that, applying a factor-of-safety of 2,
the pile head deflection at the allowable load is no more than 6.4 mm (0.25 in).
0
5
10
15
20
25
30
35
40
45
0 500 1000 1500 2000 2500 3000
Load [kN]
Top Movement [mm]
Elastic Line
Davisson Offset Limit Line
FIG 1. Load Versus Top Deflection Curve – Osceola AR Site (after Zheng et al., 2007)
DEEP FOUNDATIONS 571
571
5
Again, it is clear that the pile is capable of resisting additional compressive load
beyond the ultimate load defined by the DOL. For this project, a modifier of 4.5 was
applied to the soil quake term in the DOL equation to obtain an ultimate load value in
the range of the most conservative of the other three methods shown. A review of
recent load tests available to the authors (performed from January 2007 to August
2008) indicates that offset modifiers of between 4 and 5 are typically required to obtain
ultimate load values from the DOL that are in the range of those as calculated by the
NeSmith (2002) method.
FIG 2. Applied Load vs. Pile Head Deflection and Ultimate Load Analysis
572 DEEP FOUNDATIONS
572
6
DISCUSSION AND SUGGESTIONS
An examination of the fundamental assumptions of the DOL shows that its application
to cast-in-place piles lacks scientific basis and leads to over conservatism.
Interestingly, these are the same reasons given by Davisson for its introduction in
1973. Because of its ease in application rather than its technical merit, the DOL
continues to be widely used in the United States for the interpretation of load tests
performed on all pile types. Due to its conservatism and, arguably, over-conservatism,
the use of the DOL dramatically increases the likelihood of greater foundation costs.
The authors’ experience is that the DOL is often applied indiscriminately with an
end result of greater foundation costs unnecessarily. In light of this, the following
suggestions are offered for the load test procedure and interpretation of cast-in-place
piles:
• Ideally, load tests should be carried to a top deflection that allows the
application of the Brinch Hanson 90% Criterion, Butler-Hoy Criterion, and/or
other methods appropriate for cast-in-place piles. It is noted that most recent
version of ASTM D1143 (2007) lists the Quick Load method as the standard
compressive load test method with load to be applied in increments of about
5% of the estimated failure load and continuing until geotechnical failure.
• When the load tests are not carried to definitive geotechnical failure, the
authors recommend the rational (and limited) extrapolation of the loaddeflection
curve to allow the application of either the Brinch Hanson 90%
Criterion or the Butler-Hoy Criterion. A review of the load test data available to
the authors indicates that at pile-head deflections of about 5% of the pile
diameter, sufficient mobilization of the pile toe has occurred to allow for
reasonable extrapolation according to the method described by Chin (1970)
• In the long term, a more rational criterion for establishing the cast-in-place pile
capacity should be codified. Most notably, the L1-L2 method proposed by
Hirany and Kulhawy (1989) recognizes aspects specific to cast-in-place piles.
Furthermore, Kulhawy and Chen (2005) have combined the L1-L2 method with
the slope tangent method to allow an empirical projection of axial compressive
pile capacity.
• As a minimum (assuming none of the aforementioned changes have been
implemented), the soil quake component should be modified as proposed by
Davisson (1993) for cast-in-place piles when establishing the offset line for the
DOL.
DEEP FOUNDATIONS 573
573
7
REFERENCES
ASTM (2007) “Standard test method for piles under static axial compressive load” ASTM D
1143-07.
Brinch Hansen, J. (1963): Discussion, “Hyperbolic stress-strain response. Cohesive soils”,
Journal of Soil Mechanics and Foundations Division, ASCE, 89(SM4), 241-242.
Butler, H.D. and Hoy, H.E. (1977) “User’s manual for the Texas quick load method for
foundation load testing” FHWA-IP-77-8, Federal Highway Administration, Office of
Development, Washington, 59 pp.
Chin, F.K. (1970) “Estimation of ultimate load of piles not carried to failure” Proceedings, 2nd
Southeast Asia Conference on Soil Engineering, 81-90.
Davisson, M.T. (1972) “High capacity piles” Proceedings, Lecture Series, Innovations in
Foundation Construction, ASCE, Illinois Section, 52 pp.
Davisson, M.T. (1993) “Negative skin friction in piles and design decisions” Proceedings,
Third International Conference on Case Histories in Geotechnical Engineering, St.
Louis, 1793-1801.
Hirany, A. and Kulhawy, F.H. (1989) “Interpretation of load tests on drilled shafts – Pt. 1:
Axial compression” Fndn. Eng. Current Principles and Practices, GSP 22, Ed. Fred
Kulhawy, ASCE, New York, 1132-1149.
Kulhawy, F.H. and Chen, J-R. (2005) “Axial compression behavior of augered cast-in-place
piles in cohesionless soils” Advances in Deep Foundations ,GSP 132, ASCE.
NeSmith, W.M. (2002) “Design and installation of pressure-grouted, drilled displacement
piles” Proceedings, Ninth International Conference on Piling and Deep Foundations,
Nice, France.
Zheng, W., Hart, T.P., and Roldan, R.A. (2007) “Load test analysis on augered pressure grouted
displacement piles” Proceedings, 32nd Annual Conference on Deep Foundations,
Colorado Springs, Deep Foundations Institute, 25-36.
574 DEEP FOUNDATIONS
574